همه ما مي‌دانيم كه سطح مستطيل را مي‌توان با مربع‌هاي مساوي پوشاند به شرط آن‌كه طول ضلع‌هاي آن صحيح و مضرب طول ضلع‌هاي مربع‌ها باشند. اما چه اتفاقي ‌مي‌افتد اگر ما مجبور باشيم از مربع‌هايي با اندازه‌هاي متفاوت استفاده كنيم؟

اولين مربع مستطيل در سال 1925 توسط «زبينيف مورو» (Zbigniew Moro) كه از 10 مربع با اندازه‌هاي 3، 5 ، 6 ، 11 ، 17 ، 19 ، 22 ، 23 ، 24 ، 25 استفاده كرد.

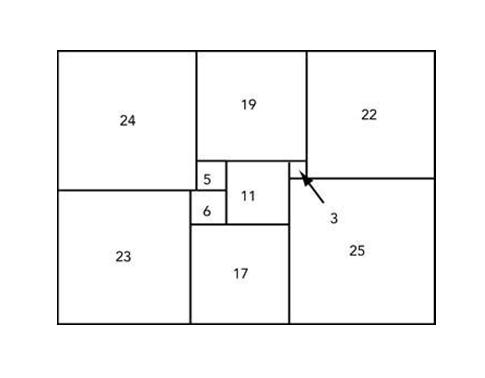
طولي نكشيد كه او با 9 مربع به سايزهاي 1 ، 4 ، 7 ، 8 ، 9 ، 10 ، 14 ، 15 و 18 توانست مربع مستطيل را بپوشاند. آيا شما مي‌توانيد اين مربع‌ها را طوري بچينيد كه مربع مستطيل را بپوشاند؟

حال چه فرقي مي‌كند اگر از مربع‌هايي با اندازه‌هاي متفاوت براي ساخت يك مربع استفاده شود؟

براي مدت طولاني بر اين تصور بودند كه اين كار غير ممكن است اما در سال 1939 ، «رولاند اسپارگو» (Roland Spargue) 55 مربع مجزا پيدا كرد كه با هم يك مربع را مي‌ساختند. 

در سال 1940، چهار رياضيدان به نام‌هاي «لئونارد بروكس» (Leonard Brooks)، «سدريك اسميت» (Cedric Smith)، «آرتور استون» (Arthur Stone)، و «ويليام توت» (William tutte) مقاله‌اي چاپ كردند در مورد مسأله «شبكه‌هاي الكترونيكي» ( شبكه‌اي كه اندازه‌هاي مربع‌ها را به كد تبديل مي‌كند و مي‌گويد چگونه در كنار هم قرار گيرند) كه باعث شد راه حل‌هاي زيادي به دست آيد.

مربع «ويلكاكس» (Willcocks) با 24 مربع، مربع‌بندي شد.

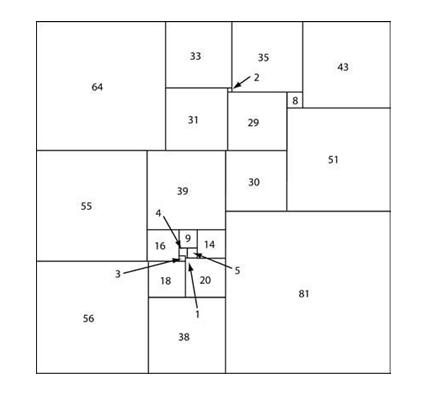
در سال 1948 ، «تئوفيلوس ويلكاك» (Theophilus Willcock) با قرار دادن 24 مربع در كنار هم توانست يك مربع بسازد. براي مدتي تصور مي‌شد كه هيچ ترتيب كوچكتري را نمي‌توان ساخت اما در سال 1962 ميلادي «آدريانوس دوجوستين» (Adrianus Duijvestin) با كامپيوتر نشان داد كه تنها به 21 مربع نيار است و اندازه آن‌ها بايد 2 ، 4 ، 6 ، 7 ، 8 ، 9 ، 11 ، 15 ، 16 ، 17 ، 18 ، 19 ، 24 ، 25 ، 27 ، 29 ، 33 ، 35 ، 37 42 و 50 باشد.

آيا شما مي‌توانيد با اين اندازه‌ها مربع «آدريانوس دوجوستين» (Adrianus Duijvestin) را بسازيد؟يك راهنمايي اين است كه اندازه اين مربع 1126112 است.

بعد از اينكه اين كار را انجام داديد، يك صطح بي‌نهايت را مربع‌بندي كنيد!!!!