زنگتفریح شماره ۱۶۵

شاید تا بهحال اسم مسالهٔ معروف «تثلیث زاویه» به گوشتان خورده باشد. مسالهای مشهور که از دوران باستان تا چند قرن پیش ریاضیدانان بسیاری را سر کار گذاشت! بله! سر کار گذاشت، زیرا افراد زیادی بخش زیادی از عمر خود را در تلاش برای حل این مساله صرف کردند و البته موفق هم نشدند، زیرا در قرن نوزدهم میلادی ثابت شد این کار امکانپذیر نیست. صورت مساله خیلی ساده است، و همانطور که از اسمش پیداست سؤال یافتن راهی است تا بتوان هر زاویهٔ دادهشده را به سه قسمت برابر تقسیم کرد، البته تنها ابزاری که مجاز به استفاده از آنها هستیم خطکش (نامدرج) و پرگار است. مثلا، همانطور که از دورهٔ راهنمایی آموختهاید، میتوان با استفاده از خطکش و پرگار یک زاویه را به دو قسمت برابر تقسیم کرد.
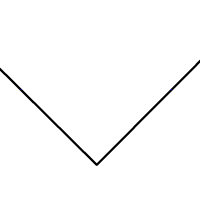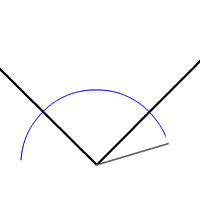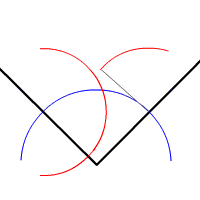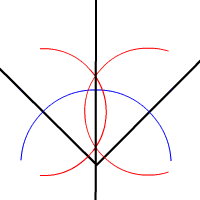
ترسیم نیمساز زاویه با استفاده از خطکش و پرگار
قرن هجدهم قرن خاصی در دنیای ریاضیات بود، ظهور یک نابغهٔ فرانسوی که عمری کوتاه ولی پربار داشت رویکرد به ریاضیات را از همه نظر تغییر داد. گالوا با طرح نظریهاش که تا سالها بهصورت معمایی عجیب در برابر سایر ریاضیدانان قرار داشت، تجردی را در ریاضیات پایهگذاری کرد که ابزاری قوی در دست ریاضیدانان شد تا با کمک آن مسالههای زیادی را حل کنند از جمله ثابت شد که تثلیث زاویه با استفاده از خطکش و پرگار ممکن نیست.
در سال ۱۸۶۶ میلادی، یک ریاضیدان فرانسوی بهنام پیِر ونزل (Pierre Wentzel) توانست ثابت کند که نمیتوان هر زاویهای را با کمک خطکش و پرگار به سه قسمت برابر تقسیم کرد. البته متأسفانه هنوز افراد زیادی هستند که سعی میکنند با استفاده از خطکش و پرگاز زاویه را به سه قسمت برابر تقسیم کنند و یا ادعای حل آن را دارند! این افراد را در محافل ریاضی با نام «نوابیغ ریاضی!» میشناسند. نیاز به گفتن نیست که نوابیغ ریاضی به خود زحمت یادگیری نظریهٔ گالوا را ندادهاند.
اما در سالهای واپسین قرن بیستم برخی از ریاضیدانان خوشذوق با استفاده از کاغذ و تا یا اریگامی هندسهای را بنا نهادند و آن را «هندسهٔ کاغذوتا» نامیدند. این هندسه اصول خاص خودش را دارد که در زیر به آن اشاره کردهایم. با استفاده از این اصول میتوان مشابه مسالههای هندسهٔ خطکش و پرگار مسالههای هندسهٔ اقلیدسی را حل کرد. مثلاً میتوان با تازدن یک زاویه بهطوری که دو ضلع زاویه روی هم بیفتند نیمساز زاویه را پیدا کرد (دقیقا محل تای کاغذ) و بدین صورت زاویه به دو قسمت برابر تقسیم میشود.
|
اصول هندسهٔ کاغذوتا*:
اصل ۱. با تا کردن کاغذ، ردی بهصورت خط راست روی آن خواهد افتاد.
اصل ۲. با تا کردن، میتوان خطی را از یک یا دو نقطه گذراند.
اصل ۳. با تا کردن، میتوان نقطهای را روی یک نقطهٔ دیگر از همان کاغذ انداخت.
اصل ۴. با تا کردن، میتوان نقطهای را روی خطی از همان کاغذ انداخت تا رد کاغذ از نقطهٔ دوم بگذرد.
اصل ۵. با تا کردن، میتوان هر خطی را روی خط دیگری از همان کاغذ انداخت.
اصل ۶. با تا کردن، میتوان پارهخطها و زاویهها را روی یکدیگر انداخت. اگر آنها همدیگر را بهطور کامل بپوشانند میتوان گفت با هم برابرند.
* این اصول بر اساس کتاب «هندسه کاغذوتا»، نوشتهٔ دنوان ا جانسون است که انجمن ملی معلمین ریاضی امریکا و کانادا آن را منتشر کرده است. در ایران پرویز امینی و امیر صالحی طالقانی این کتاب را ترجمه کردهاند و انتشارات مدرسه نیز آن را منتشر نموده است.
در منبعهای دیگر ممکن اصول دیگری برای هندسهٔ کاغذوتا نگاشته شده باشد، با این حال هر مجموعه از اصول قابل اثبات بهوسیلهٔ دیگری هستند، یعنی نتیجهٔ زیر بر اساس هر کدام از اصول درست است.
بهعنوان مثال میتوان به اصول نگاشته شده بهوسیله هوزیتا (Huzita) و هاتوری (Hatori) اشاره کرد.
|
اما یک مسالهٔ جالب در هندسهٔ کاغذوتا که وجه تمایز مهم آن از هندسهٔ خطکش و پرگار بهشمار میرود این است که میتوان با استفاده از آن و به سادگی هر زاویه را به سه قسمت برابر تقسیم کرد. در زیر روش تثلیث زاویه با استفاده از هندسهٔ کاغذ و تا را توضیح دادهایم.
 ابتدا زاویهٔ دلخواه خود را با تا زد یک گوشهٔ کاغذ مشخص میکنیم. توجه داشته باشید که کاغذ ما در ابتدا بهصورت مستطیل است. اگر کاغذ بهصورت مستطیل نباشد میتوان با استفاده از اصول کاغذوتا آن را به مستطیل تبدیل کرد. ابتدا زاویهٔ دلخواه خود را با تا زد یک گوشهٔ کاغذ مشخص میکنیم. توجه داشته باشید که کاغذ ما در ابتدا بهصورت مستطیل است. اگر کاغذ بهصورت مستطیل نباشد میتوان با استفاده از اصول کاغذوتا آن را به مستطیل تبدیل کرد. |
 |
 این زاویه را θ (بخوانید تِتا) مینامیم و هدف ما این است که با تا زدن آن را به سه زاویهٔ برابر تقسیم کنیم. این زاویه را θ (بخوانید تِتا) مینامیم و هدف ما این است که با تا زدن آن را به سه زاویهٔ برابر تقسیم کنیم. |
 |
 ابتدا بهوسیلهٔ تا زدن خطی را به موازات ضلع پایینی کاغذ مشخص میکنیم. برای این کار کافیست کاغذ را طوری تا بزنیم که ضلعهای کناری کاغذ روی خودشان بیفتند. ابتدا بهوسیلهٔ تا زدن خطی را به موازات ضلع پایینی کاغذ مشخص میکنیم. برای این کار کافیست کاغذ را طوری تا بزنیم که ضلعهای کناری کاغذ روی خودشان بیفتند. |
 |
 حال کاغذ را طوری تا میزنیم که ضلع پایینی روی خطی بیفتد که مشخص کردیم. حال کاغذ را طوری تا میزنیم که ضلع پایینی روی خطی بیفتد که مشخص کردیم. |
 |
 حال دو خط موازی با ضلع پایینی کاغذ داریم. حال دو خط موازی با ضلع پایینی کاغذ داریم. |
 |
 در این مرحله، همانطور که در شکل میبیند، باید کاغذ را طوری تا بزنید که راس سمط چپ از پارهخط بالایی روی ضلع زاویه بیفتد، بهطوریکه راس زاویه هم همزمان روی پارهخط پایینی قرار بگیرد. در این مرحله، همانطور که در شکل میبیند، باید کاغذ را طوری تا بزنید که راس سمط چپ از پارهخط بالایی روی ضلع زاویه بیفتد، بهطوریکه راس زاویه هم همزمان روی پارهخط پایینی قرار بگیرد. |
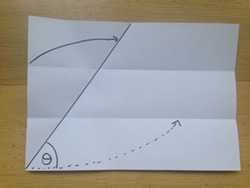 |
 نتیجهٔ کار را در شکل میبینید. نتیجهٔ کار را در شکل میبینید. |
 |
 در این مرحله یکی از خطهایی که یکسوم بالایی زاویه را مشخص خواهد کرد را پیدا میکنیم. برای این کار کاغذ را از روی رد تای پارهخط پایینی به سمت پایین تا میزنیم. در این مرحله یکی از خطهایی که یکسوم بالایی زاویه را مشخص خواهد کرد را پیدا میکنیم. برای این کار کاغذ را از روی رد تای پارهخط پایینی به سمت پایین تا میزنیم. |
 |
 در شکل رد تای جدید با رنگ قرمز مشخص شده است. در شکل رد تای جدید با رنگ قرمز مشخص شده است. |
 |
 حال کاغذ را کامل باز میکنیم و با تا زدن در راستای خط قرمز، امتداد آن را به راس زاویه میرسانیم. حال کاغذ را کامل باز میکنیم و با تا زدن در راستای خط قرمز، امتداد آن را به راس زاویه میرسانیم. |
 |
 با باز کردن کاغذ شکلی شبیه این باید داشته باشید. با باز کردن کاغذ شکلی شبیه این باید داشته باشید. |
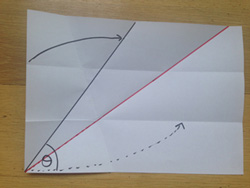 |
 در مرحله آخر با تا زدن، ضلع پایینی کاغذ را روی خط قرمز بیندازید. در مرحله آخر با تا زدن، ضلع پایینی کاغذ را روی خط قرمز بیندازید. |
 |
 با باز کردن کاغذ زاویهٔ تقسیم شده به سه قسمت را خواهید دید. با باز کردن کاغذ زاویهٔ تقسیم شده به سه قسمت را خواهید دید. |
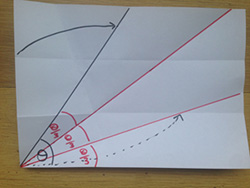 |
آیا میتوانید درستی این ادعا را اثبات کنید؟