زنگتفریح شماره ۱۱۶
میخواهیم یک مربع جادویی بزرگ بسازیم. حتما با مربعهای جادویی آشنا هستید، مربع جادویی n در n جدولی از عددهای طبیعی از ۱ تا n2 است که حاصل جمع همهی عددهای هر سطر و هر ستون با هم مساویاند. در شکل زیر میتوانید یک مربع جادویی ۳ در ۳ را ببینید:
در یک مربع جادویی n در n حاصل جمع عددهای هر سطر یا ستون برابر است با
|
(۱+۲+۳+...+n۲)/n = (n۲/۲)(n۲+۱)/n = (n/۲)(n۲+۱)
|
مثلا اگر به مربع جادویی ۳ در ۳ بالا دقت کنید حاصل جمع هر سطر یا ستون برابر است با ۱۵. بهراحتی میتوان دید که نمیتوان مربع جادویی ۲ در ۲ ساخت. (چرا؟!) حال میخواهیم مربعهای جادویی بزرگتری بسازیم. فرض کنید یک مربع جادویی n در n و یک مربع جادویی m در m داشته باشیم، میخواهیم یک مربع جادویی mn در mn بسازیم. نکتهای که برای ساخت این مربع جادویی از استفاده میکنیم این است که اگر همهی عددهای یک مربع جادویی n در n را با یک عدد ثابت c جمع کنیم، حاصل مربعی خواهد شد که حاصلجمع عددهای هر سطر و ستون با هم مساوی خواهند شد. (این حاصلجمع برابر با n/۲)(n۲+۱) + nc) )
اکنون بهسادگی خواهید توانست یک مربع جادویی nm-در-nm بسازید:
ابتدا از روی مربع جادویی n-در-n، بهتعداد m۲ مربع با جمع کردن عددهای مربع بهترتیب با
|
0*m2, 1*m2, 2*m2, ... , (m2-1)m2
|
میسازیم. کاری که باقی میماند این است که مربع اول را جایگزین خانهای از مربع جادویی m-در-m کنیم که در آن عدد ۱ قرار گرفته است، و به همین ترتیب مربع k*m2 را جایگزین خانهای کنیم که عدد k+۱ قرار گرفته است. بهاین ترتیب مربع جادویی nm-در-nm ساخته میشود.
بهعنوان مثال ما با استفاده از مربع جادویی ۳ در ۳مان یک مربع جادویی ۹ در ۹ ساختهایم:
البته در مربع بالایی عددها از صفر شروع شدهاند، برای ساختن یک مربع جادویی، هر یک از عددهای بالا را با ۱ جمع می کنیم.
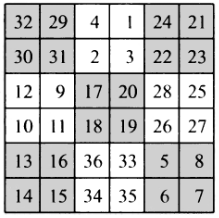
همانطور که در بالا هم اشاره کردیم مربع جادویی ۲در۲ نداریم، پس این روش ممکن است زیاد بهدرد ساختن مربعهای جادویی از ضریب ۲ نخورد، ولی در برخی مواقع میتوان با کمی کلک زدن از این روش استفاده کرد،مثلا در زیر میتوانید مربع جادویی ۶در۶ را ببینید که از این روش برای ساختن آن کمک گرفته شده است، اما چون مربع ۲در۲ در اختیار نداشتهایم، این کار را با استفاده از دو حالت مختلفی که عددها را در مربع ۲در۲ نوشتهایم انجام دادهایم، با کمی دقت میتوانید روش ساخت این مربع جادویی را حدس بزنید.