در بند بعد خواهیم یافت که صفحه را نمی‌توان به‌کمک چندضلعی‌های محدب هم‌نهشتی که هفت ضلع یا بیشتر دارند فرش کرد. اما در مورد چندضلعی‌های مقعر وضع به‌گونه‌ی دیگری است.

در شکل زیر یک هشت‌ضلعی مقعر دیده می‌شود که می‌توان به‌کمک آن صفحه را فرش کرد ( هشت‌ضلعی ABCDEFGH).

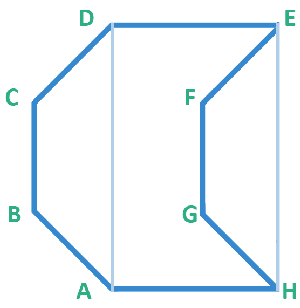
پاره‌خط‌های راست DE و  AH موازی و برابر یک‌دیگرند و چهار‌ضلعی‌های ABCD و HGFE هم‌نهشتند. اگر پاره‌خط‌های راست AD و HE را رسم کنیم، مستطیل ADEH به‌دست می‌آید. این مستطیل، فرورفتگی HGFE از هشت‌ضلعی را پر و بخش ABCD از آن را حذف می‌کند. در ضمن، مستطیل ADEH، مساحتی برابر با مساحت هشت‌ضلعی و محیطی کمتر از محیط آن دارد، در نتیجه، نسبت هم پیرامونی در مستطیل ADEH، بزرگتر از نسبت هم پیرامونی برای هشت ضلعیABCDEFGH  است. علاوه براین، روشن است که، هر مستطیلی، برای فرش کردن صفحه، مناسب است.

به این ترتیب، بین چندضلعی‌های منتظم، چندضلعی‎های مقعری که برای فرش کردن مناسبند، شش‌ضلعی‌های منتظم بزرگ‌ترین نسبت هم‌پیرامونی را دارد. تنها این مطلب باقی می‌ماند که چندضلعی‌های محدب را هم مطالعه قرار دهیم.

از هر مثلث دل‌خواهی می‌توان، برای فرش کردن صفحه استفاده کرد. همین حکم درباره‌ی چهارضلعی دل‌خواه  هم درست است. احکام ساده‌ای است که انتظار می‌رود خواننده خود آنها را اثبات کند. برخی از پنج‌ضلعی‌های محدب (البته، نه همه‌ی آن‌ها)، برای فرش کردن صفحه مناسبند، به همین ترتیب در مورد شش‌ضلعی‌های محدب، مساله مربوط به شش‌ضلعی‌های محدبی که برای سنگ‌فرش مناسبند کاملا حل شده است، ولی مساله‌ی مشابه آن، برای پنج‌ضلعی‌های محدب، هنوز به‌طور کامل حل نشده است.

نمونه‌ای از شش‌ضلعی‌های محدب، که برای فرش کردن صفحه مناسبند، شش‌‎ضلعی منتظم است. به‌کمک همین شش‌ضلعی منتظم، می‌توان نمونه‌ای از پنج‌ضلعی محدب را، که برای فرش کردن صفحه قابل استفاده باشد، به‌دست آورد. برای این منظور، کافی است مثلا وسط‌های دو ضلع روبه‌رو از شش‌ضلعی منتظم را، با پاره‌خط راستی، به یک‌دیگر متصل کنیم، در این صورت، شش‌ضلعی مفروض به دو پنج‌ضلعی هم‌نهشت تبدیل خواهد شد که برای فرش کردن صفحه مناسبند. ولی، همان‌طور که اشاره شد، هنوز این مساله حل نشده است که، یک پنج ضلعی محدب دل‌خواه، با چه شرایطی می‌تواند برای فرش کردن مورد استفاده قرار گیرد.

فرش کردن صفحه با چند ضلعی های محدب
در مورد فرش کردن صفحه با چند‌ضلعی‌های محدب، قضیه زیر را داریم:

ما به اثبات این قضیه نمی‌پردازیم. برای اثبات، خواننده می‌تواند از کتاب مرجع استفاده کند. «لازم به ذکر است که اثبات مقدماتی اما طولانی در مرجع مورد استفاده موجود است».

از آن چه در این دو زنگ‌تفریح اشاره شد، می‌توان نتیجه گرفت که:

از بین همه‌ی چند‌ضلعی‌هایی که برای فرش کردن صفحه مناسبند. شش‌ضلعی منتظم، بیش‌ترین نسبت هم‌پیرامونی را دارد. یعنی دارای بیش‌ترین مساحت با محیط مفروض است. آخرین قضیه نشان می‌دهد برای فرش کردن صفحه نمی‌توان از چندضلعی‌هایی با بیشتر از یا مساوی هفت ضلع استفاده کرد. همچنین در بند فرش کردن با چندضلعی‌‍های مقعر دیدیم که احتمال پوشاندن صفحه با این چند‌ضلعی‌ها وجود دارد، ولی در هر حال، می‌توان چندضلعی محدبی با نسبت هم‌پیرامونی بزرگ‌تر، برای پوشاندن صفحه پیدا کرد (درست است که اثبات را به‌کمک یک مساله‌ی خاص انجام دادیم، ولی می‌توان آن را تعمیم داد. تعمیم‌های بدیهی را به خواننده واگذار می‌کنیم « هرشتاین»).

حال نوبت چندضلعی‌هایی که با 3، 4، 5 و 6 ضلع باشند، می‌رسد. به آسانی می‌توان مشاهده کرد که در بین مثلث متساوی‌الاضلاع و چهارضلعی‌ها، مربع دارای بیش‌ترین نسبت هم‌پیرامونی است. نتیجه‌ی مشابهی برای شش‌ضلعی‌ها برقرار است. همچنین روشن است که نسبت هم‌پیرامونی برای چندضلعی‌ها با افزایش n، بزرگتر می‎ شود.

و اما درباره‎ی پنج‎‌ضلعی‎های محدب، به‎آسانی ثابت می‎شود در بین همه پنج‎ضلعی‎ها، پنج‌ضلعی منتظم بزرگ‌ترین نسبت هم‌پیرامونی را دارد. همچنین می‌توان ثابت کرد یک پنج‌ضلعی با نسبت هم‌پیرامونی بزرگ‌تر وجود دارد. البته برای هر پنج‌ضلعی یک شش‌ضلعی با نسبت هم‌پیرامونی بزرگ‌تر وجود دارد، گرچه می‌توان حالت کلی تر را نیز در نظر گرفت و ثابت کرد: 

مراجع:
 Maxima and Minima without Calculus by Ivan Niven.