با وجود نام «بازي» (Game) زماني كه «جان كانوي» (John Conway) فرايندي – كه خودش بهنام «زندگي» (Life) ناميده بود – توسعه داد بههيچ وجه قصد نداشت «زندگي» را شبيهسازي كند. اين همه در حالي است كه طبيعت زندگيگونهي «بازي» با پيچيدگيها و عدم امكان پيشبينيهاي پايانناپذيرش تصورها از همهي دنيا را تسخير كرده است.
هدف اصلي «جان كانوي» (John Conway) كاملاً جنبهي رياضي داشت. وي سعي كرد فرايندي را كشف كند كه به «فرايند جهانشمول» (Universal System) شهرت يافت. بدينمعنا كه فرايندي از مجموعهاي از كامپيوترهاي قابلبرنامهريزي كه قادر باشد محاسبههاي دلخواه را انجام دهد.
در دههي 1330 (1950 ميلادي) يكي از پيشتازان حوزهي «اتوماتاي سلولي» (Cellular Automata) موفق به خلق يك فرايند جهانشمول شد. فرايند وي در حوزهي «اتوماتاي سلولي» (Cellular Automata) در يك صفحهي دوبعدي قرار داشت البته در حالتي كه وابستگي هر سلول در زمان تنها به حالت همسايگانشان در زمان باشد.
فرايند «ون نويمان» (Von Neumann) بهصورتي باورنكردني پيچيده بود زيرا به 29 حالت احتياج داشت كه از چگونگي ناشي شدن از فرايند مذكور نتيجه گرفته شده بود. «جان كانوي» (John Conway) فرايند «ون نويمان» (Von Neumann) را – كه براي توسعهي اين فرايند پيچيده بهكار ميرفت – چنين توصيف كرد:
«اگر وي به توانايي خاصي (مانند: توانايي انتقال پيام) نياز داشت چند حالت بيشتري به آن ميافزود و بنابراين به 29 حالت دست پيدا ميكرد. پيوست مقالهاش را فهرست بلندبالايي از «جداول انتقال» (Transmit Tables) تشكيل ميداد ... اين يك پيام واقعي محسوب ميشود».

|
|
 |
شكل 5 - «ون نويمان»
(Von Neumann). |
در مقام مقايسه، هدف «جان كانوي» (John Conway) يافتن فرايندي «جهانشمول» و در عين حال بهطور قابلتوجهي «ساده» بود. بهجاي اينكه بهطور واضح فشار بر روي فرايند مذكور براي بروز رفتار مطلوب ]هدف «ون نويمان» [(Von Neumann) اعمال كند وي اعتقاد داشت كه بهترين راه، انتخاب فرايندي با رفتار بهظاهر مناسب و زندگي با آن در تمام مواقع و يادگيري چگونگي برنامهريزي آن است تا محاسبههاي دلخواه اعمال شود.
|
شكل 6 – آيا فرايند جهانشمول است؟ |
«جان كانوي» (John Conway) ميگويد: «بهعنوان مثال، تمام بيتهاي الكترونيكي را برداشته آنها را بهصورت تصادفي در يك «مخزن» (Warehouse) به يكديگر متصل كنيد. سپس احتمالاً ماشيني جهانشمول بهدست خواهيد آورد». اين تنها موضوعي از زندگي داراي فرايند و چگونگي كاركرد آن است.
«جان كانوي» (John Conway) همچنين گفته است: «ممكن است كليدي را در اينجا بفشاريد و متوجه شويد كه نوري كمرنگ با رنگ قرمز پديدار ميشود؛ سپس تلاش كرده ميفهميد كه چگونه اين كليدها به اين چيزها بستگي دارند. بدينترتيب روش جمع دو عدد را مييابيد. شما اين كليد را پنجبار فشرده و سپس كاري ديگر انجام ميدهيد. بعد آن كليد را هشتبار ديگر ميفشاريد و بدينترتيب جواب 13 ظاهر ميشود و اگر «مخزن» (Warehouse) بهاندازهي كافي بزرگ بوده و آن رفتار بهاندازهي كافي جالب باشد بهتدريج ميآموزيد چگونه از بيتهاي كوچك آن استفاده كنيد تا آنچه را كه دوست داريد انجام دهيد. اين امري رؤيايي است.
سؤالهايي كه هماكنون مطرح است مواردي نظير ذيل است:
| - آن «مخزن» (Warehouse) را چقدر كوچك ميتوان ساخت؟ |
| - ارتباطها را چقدر «ساده» ميتوان ايجاد كرد؟ |
|
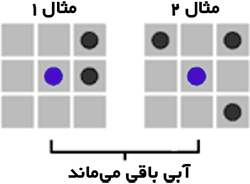
الف - يك سلول «زنده» اگر دو يا سه همسايه
داشته باشد با تكثير بعدي زنده ميماند. |
|
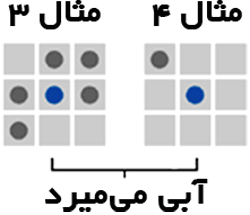
ب - يك سلول زنده اگر چهار يا بيشتر همسايه
داشته باشد (دچار ازدحام شده باشد)
يا اگر داراي تنها يك همسايه يا تنها باشد
[«انزوا» (Isolation)] ميميرد. |

|
ج - يك سلول زنده اگر داراي دقيقاً
سه همسايه باشد در تكثير بعدي
يك سلول زنده ميشود. |
|
شكل 7 - قواعد زندگي با ...
«زندگي» بازياي بر شبكهاي از
مربعهايي است كه در آن هر سلول يا زنده
و «اشغال شده» (Occupied) است
يا «مرده» و «خالي» (Empty) است.
شما با يك سازگارياي از
سلولهاي «زنده» آغاز ميكنيد
و اين بازي با تكثير سلولهاي «زنده»
پيش رفته قواعد مرگ در مورد آن
اعمال ميشود. |
«زندگي» بهسادگي آنچه «جان كانوي» (John Conway) اميد دارد نيست اما وي از آن با عنوان: «انواعي از شكستها» (A Sort of Failures) نام برد. بنابر يك ديدگاه، فرايند «ون نويمان» (Von Neumann) «سادهتر» است بهگونهاي كه حالت يك سلول تنها به خودش و همسايگان ضربدرياش بستگي دارد در حالي كه «زندگي» درون همهي هشت همسايهاش احاطه شده است.
«جان كانوي» (John Conway) بهطوري ايدهال در جستجوي فرايندي بود كه «بهطور شگفتاوري ساده» محسوب ميشد؛ يكي اينكه داراي يكبعد باشد يعني «اتوماتاي سلولي» (Cellular Automata) بيشتر در يك خط است تا يك صفحه.
«جان كانوي» (John Conway) ميگويد: «با يك فرايند دوبعدي شما مجبور هستيد موقعيت را در زمان نگه داريد. اگر بتوانيم پيچيدگي فضايي را كه در آن كار ميكنيم كاهش دهيم بهتر خواهد بود».
سختترين مرحله پيدا كردن فرايندي دوبعدي براي تحقيق است. اگرچه چنين فرايندهايي در يك صفحهي نامحدود انجام ميشود تحقيق دربارهي آنها مستلزم مشاهدهي بخشي محدود از آن صفحه است.
گروه پژوهشي «جان كانوي» (John Conway) از «تابلوهاي حركت» (Go Boards) براي توسعهي «زندگي» (Life) استفاده كردند و بهمنظور اينكه قادر باشند يك فرايند را مطالعه كنند لازم است آن گروه تمايل به:
| - گسترده كردن |
| - و كار مستقل (Race off) بر روي |
آن تابلوها نداشته باشند. اين بدينمعنا است كه آنها مجبور بودند بعضي از انواع قواعد «مرگ» (Death) را بر آن فرايند تحميل كنند.
البته يك فرايند بايد داراي رفتاري بهاندازهي كافي جالبتوجه باشد تا براي «فرايند جهانشمولي» (Universal System) شانس داشته باشد بهگونهاي كه اهميت يكساني داشته و آن جمعها بنابر قاعدهي «تولد» بهطور معمول نميرند.
«جان كانوي» (John Conway) ميگويد: «ما با انواع قواعد براي مطالعهي تأثيرشان بازي كرده و آنچه را كه اتفاق ميافتد مشاهده مينماييم. موارد:
| - يا بهصورت وحشتناكي تمايل به گسترده شدن دارند |
| - يا اينكه تمايل دارند بهتدريج ناپديد شوند. |
لذا اين سؤال مطرح ميشود: چگونه ميتوانيد «توانهاي نسبي» (تعداد سلولهايي را كه يك سلول را احاطه كردهاند) (Relative Strengths) مربوط به قوانين «زندگي» و «مرگ» (Death Rules) را معين كنيد بهگونهاي كه (براي يك جمعيت نمونه) احتمال نسبياي وجود داشته باشد كه آنها دچار مرگ نشده و هريك داراي رشد خطي (Linear) نباشند».
مشكل واقعي عبارت از پيدا كردن «توانهاي نسبي» (Relative Strengths) صحيح از اين قواعد است؛ بدينمنظور كه فرايند هم بهاندازهي كافي براي مطالعه جالب بوده و بهقدر كافي زندگي با آن مناسب باشد.
|
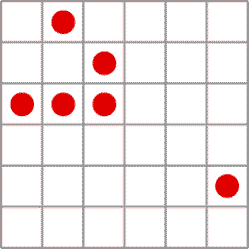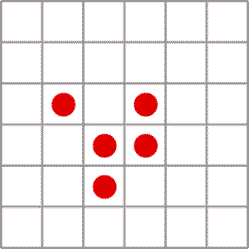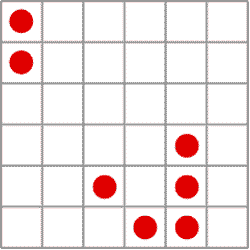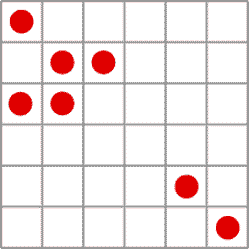
شكل 8 – گشت و گذار گلايدرها
در اطراف هواپيما. |
«كانوي» (Conway) و گروهي از فارغالتحصيلان بعد از متجاوز از دو سال بحث و گفتگو با قواعد «مرگ» و «زندگي» آزمايشهايي را ترتيب دادند. زماني كه آنها وارد مجموعهاي از قواعدي شدند كه «زندگي» ايجاد شد بهسرعت عمليات «رفع اشكال» (Thinkering) را متوقف كردند.
زندگي با چنين فرايندي بهزودي نشان داد كه وجود نحوهي قرارگيري - كه گروه پژوهشي تصميم گرفتند آنها را «گلايدرها» (Gliders) يعني پيكربنديهاي گردش در اطراف هواپيما بنامند – اولين نشانهي موفقيت بوده است.
بهمنظور اثبات جهانشمولي (Universality) و نشان دادن اينكه يك فرايند قابليت محاسبههاي دلخواه را دارد لازم است روشهايي براي ارسال اطلاعات از هواپيما از يك پيكربندي (Configuration) به پيكربندي ديگر وجود داشته باشد.
«كانوي» (Conway) ميگويد:
«زماني كه چنين فرايندي بهطور كامل كشف شد همگي انجام آزمايش را با هر قواعد ديگري متوقف كرديم زيرا واضح بود هدف اين بود كه اين كار بايد «عملي» ميشد. اين فرايند دقيقاً «رفتار مورد انتظار» ما را اجرا كرده و اقدام به اثبات اين امر نموديم كه اين فرايند كار ميكند».
هفتهها گذشت تا «گروه» تمام پيكربنديها كاملاً شبيه به اجزاي يك كامپيوتر دلخواه براي محاسبههاي دلخواه ايجاد شد:
| - گيتهاي And (And Gates) |
| - گيتهاي Or (Or Gates) |
| - و ... |
اما بههر حال چيزي كه هنوز به آن دست نيافته بوديم منبع اوليه از «گلايدرها» (Gliders) محسوب ميشد كه گروه پژوهشي آن را «تپانچهي گلايدر» (Glider Gun) ناميد. وقتي به اينجا رسيديم من تقريباً نتايج اين كار پژوهشي را علني كردم».
 |
شكل 9 – «مارتين گاردنر»
(Martin Gardner). |
«جان كانوي» (John Conway) به «مارتين گاردنر» (Martin Gardner) نامه نوشته مطلبي با عنوان «زندگي» (Life) را براي قسمت ستون «بازيهاي رياضي» (Mathematical Games) در مجلهي «ساينتيفيك امريكن» (Scientific American) تقديم وي كرد؛ جايزهي 50 دلاري به وي بهخاطر پيكربندياي كه گرايش به «بينهايت» (Infinity) داشت اهدا شد.
مطلب ارائه شده در ستون مذكور، جرقهاي براي تصور عمومي شد و خيلي زود «تپانچهي گلايدر» (Glider Gun) توسط گروهي در دانشگاه «ام. آي. تي.» (MIT) بهسرپرستي «ر. و. گاسپر» (R. W. Gasper) كشف شد. در طي دو هفته از كشف «تپانچهي گلايدر» (Glider Gun) هم گروه پژوهشي «كانوي» (Conway) و هم گروه پژوهشي در دانشگاه «ام. آي. تي.» (MIT) نشان دادند كه اين فرايند جهانشمول بوده و «اين داستاني بزرگ از يك موفقيت است» (It was a Great Success Story).
از زماني كه براي اولين بار در ستون «گاردنر» (Gardner) مطالب در اختيار همگان قرار گرفت «زندگي» (Life) مقدار زيادي از علايق عمومي را شبيهسازي كرد. در يك مقطع زماني، ارتش امريكا «ارزش زماني» (Time Value) را كه براي مشاهدهي بازي «زندگي» (Life) تلف شده بود ميليونها دلار براورد كرد و اعلام كرد هنوز اتلاف آن براي «بازي» ادامه دارد.
«كانوي» (Conway) از اينكه «بازي» (Life) توانسته بود علايق و توجه مردم را به خود جلب كند خشنود بود.
«جان كانوي» (John Conway) ميگويد: «من هميشه در حال تلاش براي عرضهي رياضيات به عموم مردم هستم تا آنها را در جامعه جاري كنم». شايد باعث خوشبختي باشد كه «كانوي» (Conway) فرايندي دوبعدي را نسبت به فرايند يكبعدي توسعه داد بهگونهاي كه هماكنون بازي «زندگي» (Life) در صفحهي دوبعدي بهطور كامل اجرا شده و بدينترتيب مردم را به يكديگر مرتبط ميكند.
طبيعت زندگيگونهي بازي «زندگي» (Life Game) توجه مردم را كاملاً تسخير كرده و اگرچه «زندگي مقلدانه» واقعاً هدف نيست از يك جهت، «زندگي مصنوعي» (Artificial) هدف قرار گرفته است.
«جان كانوي» (John Conway) ميگويد: «اعتقاد دارم اگر داراي پيكربندياي بهاندازهي كافي بزرگ باشيد سيري تكاملي در صفحه مشاهده خواهيد كرد. آنچه اتفاق خواهد افتاد آن است كه هرچند وقت يكبار داراي قابليت خلاقانهاي براي بازسازي خود و سپس شروع به استقرار در صفحهي مذكور خواهيد بود.
غير از آن، صفحهي مذكور بايد با خرت و پرتهايي پر شود كه ممكن است بعضي از آنها اقدام به قتل كنند. بنابراين بعضي از آنها بهتر تجهيز ميشوند تا جان سالم بهدر ببرند. حتي هرچند وقت يكبار با ديگران ممكن است با ديگران تصادف كرده، آسيب خورده و شروع به تغيير كنند. اكثر اين تغييرها احتمالاً براي «بدتر كردن» انجام ميشود اما هرچند وقت يكبار ممكن است براي «بهتر شدن» صورت گيرد. بدينترتيب شما از «داستان» مطلع خواهيد شد.
شما ممكن است با سير تكاملياي مواجه شويد كه واقع ميشود و بدينترتيب مخلوقهايي را بهدست خواهيد آورد كه واقعاً استحقاق دارند كه نام «زنده» (Living) را بر آنها بگذاريم».
«جان كانوي» (John Conway) حتي تصور ميكند اگر بازي «زندگي» (Life) ادامه يابد و تا مدتي طولاني اين بازي اجرا شود اين مخلوقها ممكن است نهايتاً به هوشياري دست يابند!
اگرچه اين قواعد يادبودي از آن مواردي است كه در زندگي واقعي يافت ميشود هدف «كانوي» (Conway) تقليد زندگي بهشكلي كه ميدانيم نبود.
وي ميگويد: «بسياري از مردم چيزهايي از اين دست درست كردهاند كه به زندگي واقعي نزديكتر است بهعنوان مثال ميتوان به رشتههاي «دي. ان. اي.» (DNA) در يك مدل اشاره كرد. اين در تضاد با فلسفهي من است بهدليل اينكه از «مكانيسم مولدي» (Reproductive Mechanism) تقليد ميكند كه ما داريم. فلسفهي من «شروع با هيچچيز» و «ديدن» است البته اگر داراي «مكانيسم مولدي» (Reproductive Mechanism) در خودش باشد. بهخاطر اينكه من واقعاً علاقهمند به آنچيزي نيستم كه ما را مقلد ميكند. من هميشه اين عقيده را دارم كمي كوتهنظري است كه اينقدر علاقهمندي در ما وجود داشته باشد.
زماني كه مردم كرهي مريخ را ملاقات ميكنيم چه اتفاقي خواهد افتاد؟! منظورم از اين مثال كسي خارج از آنجا است كه از زندگي هوشمندانهاي برخوردار باشد.
دليل واضحي وجود ندارد كه چرا آنان از «دي. ان. اي.» (DNA) براي دستهبندي اطلاعات (Sorting)، بازسازي و ... استفاده ميكنند. آنها احتمالاً يك فرايند كاملاً متفاوت خواهند داشت.
احساس ميكنم چيزهاي انتزاعي رياضياي كه من به آنها علاقهمند هستم احتمالاً به افرادي نزديكتر هستند كه مريخيها به آن علاقهمندند. چيزهاي «غيررياضياي» كه به آن علاقهمند هستم عبارت است از «زبان انگليسي» كه مردم مريخ قصد ندارند چيزي دربارهي اين زبان بدانند؛ من چيزهايي را دوست دارم كه مريخيها به آن علاقهاي ندارند.
اما فكر ميكنم ما احتمالاً داراي علايق مشتركي باشيم. علايق مشترك ما جنبهي رياضي خواهد داشت».

|
شكل 10 – زبان جهانشمول رياضي. |
اگرچه «جان كانوي» (John Conway) اعتقاد دارد «مريخيها به «فيزيك» همچنان علاقهمند باقي بمانند همانگونه كه ما همان دنياي فيزيكي را بهاشتراك گذاشتهايم؛ نتايج طرح «رياضي» بهعنوان علاقهي مشترك آن است كه به ابزار گرانقيمتي براي دستيابي به اكتشافها نياز ندارد. مغز بهتنهايي همهي آنچيزي است كه براي مطالعهي «رياضيات» نياز است (يعني به ابزار ديگري نياز نيست) و همانطور كه «كانوي» (Canway) ميگويد وي ميتواند «در حالي كه بر روي يك صندلي راحتي، داخل حمام يا تختخواب قرار دارد بهتحقيق در اين باره بپردازد»! و علاوه بر اين، دنياي رياضيات تنها محدود به منطقهاي خاص نيست يعني داراي محدوديت مكاني نيز نميباشد.
وي ميگويد: «اگرچه ميتوانم تنها بنشينم و بر روي موضوعي جهانشمول و انتزاعي تحقيق كنم. اين مسأله در مورد همكاران پژوهشي من هم صادق است. يك ثباتي در اين زمينه وجود داشته و من واقعاً اعتقاد دارم اين موضوع انتزاعي براي مريخيها نيز قابلدرك محسوب ميشود.
«جان كانوي» (John Conway) ميگويد: «هميشه علاقهمند به اين موضوع انتزاعي بودهام و دليلش آن است كه نميفهمم چرا اينگونه است. درك نميكنم چرا قضايا تغيير نميكنند. ما اكنون ميتوانيم «قضيهي فيثاغورث» (Pythagoras’s Theorem) را آنهم تنها بيش از 200 سال از كشف آن ثابت كنيم».
«كانوي» (Conway) حتي مفهوم «منطق» براي ارتباط (Logic for Granted) را اتخاذ نميكند. اگرچه وي همانند يك رياضيدان هر روز با منطق و استدلال سر و كار دارد. او از اساسي بودن اصول موضوعه در منطق سؤال ميكند.
وي ميگويد: «من خيلي دوست دارم بدانم مريخيها به چه چيزي فكر ميكنند. آيا آنها واقعاً بههمان روشي كه ما انجام ميدهيم فكر ميكنند؟ آيا منطق آنها با ما يكي است؟!»
افتخاراميزترين كشف «كانوي» كه براي وي لذتبخش بوده است عبارت است از:
| - كشف نوع جديدي از اعداد بهنام «اعداد سورئال» (Surreal Numbers) |
| - فكر كردن دربارهي اينكه چنين كشفي در دنياي انتزاعي همانند: «قضيهي فيثاغورث» براي هزاران سال باقي ميماند. |
وي اين اعداد را بعد از مشاهدهي رقابتهاي «حركت بريتانيايي» (British Go) در دپارتمان رياضيات در دانشگاه كمبريج كشف كرد.«كانوي» (Conway) ميگويد: «در رقابتهاي حركت بريتانيايي (British Go) متوجه شدم در پايان يك بازي تمايلي جمعي براي خاتمهي بازي وجود دارد. بههمين علت بود كه فكر كردم اگر آن نظريه را توسعه بدهم ممكن است «حركت» (Go) را كمي بهتر بفهمم».
«كانوي» (Conway) در اين راه قدم گذاشت و كشف كرد كه بعضي موقعيتها همانند «اعداد» رفتار ميكنند. وي چنين ادامه ميدهد: «مطالب بيشتري نيز كشف كردم اينكه اگر در حال اجراي بازيهاي بينهايتي باشيد بعضي موقعيتها مانند يك «نوع جديد از اعداد» عمل ميكنند! اينگونه بود كه موفق به كشف اعداد «سورئال» (Surreal Numbers) شدم.

|
|
|
|

|
شكل 11 – بازي «حركت» (Go). |
از يك جهت، كشف اعداد «سورئال» (Surreal Numbers) توسط «كانوي» (Conway) با توسعهي بازي «زندگي» (Life) همراه بود. وي به مطالعهي يك فرايند تصادفي (Random System) پرداخته و در حالي كه وي با آن زندگي ميكرد به كشف دنياي شگفتانگيز پرداخت.
«جان كانوي» (John Conway) ميگويد: »هميشه اين امر براي من كمي معجزه محسوب ميشد. من با بازي «حركت» (Go) شروع كرده و با اعداد «سورئال» (Surreal) بهپايان بردم كه دنيايي بينهايت عظيم است. فكر ميكنم مريخيها هم در جايي شايد در خارج از كهكشان ما، اعداد «سورئال» (Surreal) را كشف كرده باشند ... در آن وضعيت ما به بعضي از انواع ارتباطهاي هوشمندانه دست خواهيم يافت. آن رياضيدان مريخي ناشناس ميتواند «جان كانوي مريخي» (The Martian John Conway) باشد!»
چنين ارتباطي ارزش افزودهاي از جهان انتزاعي رياضي بههمراه خواهد داشت زيرا حقايقي غيروابسته به انسان را عرضه خواهد كرد. سپس دوباره «كانوي» (Conway) فكر ميكند كه تمام مفهوم دنياي انتزاعي بهاشتراك گذاشته شده ممكن است نادرست باشد!
«كانوي» (Conway) ميگويد: «تمام سؤال موجوديت رياضي مرا فريفتهي خود كرده است! شايد مريخيها داراي ادراك يكسان از موجوديت رياضي - همانگونه كه ما درك ميكنيم - نباشند اما هرچه باشد خيلي جالبتوجه است!»