 سؤال سؤال
 در جنگلی 9 حیوان در لانههایاشان زندگی میکنند و دقیقاً یک راه جداگانه بین هر دو تا از این لانهها وجود دارد. در جنگلی 9 حیوان در لانههایاشان زندگی میکنند و دقیقاً یک راه جداگانه بین هر دو تا از این لانهها وجود دارد.
پیش از مراسم انتخاب «سلطان جنگل»، برخی از حیوانات در مبارزهی انتخاباتی شرکت ميکنند. هر نامزدي به هریک از لانههای دیگر دقیقاً یکبار سر میزند؛ فقط از راههای میان لانهها برای رفت و آمد استفاده میکند.
هیچگاه در مسیر بین دو لانه از هیچ راهی به راهی دیگر نمیپیچد و در پایان مبارزهي انتخاباتی به لانهی خودش باز میگردد.
همچنین میدانیم که هیچ راهی بین دو لانه را بیش از یک نفر از نامزدها طی نکرده است.
تازه همهی این مطالبي كه گفته شد صورت مسابقه بود!
اما سؤال ما چیست!؟
باید بیشترین تعداد نامزدها را پیدا کنید؟
 راهنمایی راهنمایی
مسأله را بهزبان«گراف» بر گردانید و فرض کنید که هر لانه یک رأس باشد و هر راه میان دو لانه،«یالی» بوده که این دو رأس را بههم وصل میکند.
 جواب جواب
مسأله را بهزبان گراف برمیگردانیم. فرض کنید که هر لانه یک راس باشد و هر راه میان دولانه (دو رأس) یالی باشد که این دو رأس را بههم وصل میکند.
به این ترتیب گراف کامل را بهدست میآوریم. بیشترین تعداد دورهای همیلتونی در این گراف کامل را میخواهیم که یال مشترک نداشته باشند (هیچ راهی بین دو لانه را بیش از یکنفر نامزد طی نکرده است). بهسادگی میتوان تحقیق کرد که تعداد دورهای همیلتونی در این گراف، از تعداد رأسها کمتر است. بنابر این همواره میتوانیم برای هر دور همیلتونی، یک نامزد انتخاب کنیم. نتیجهی کلی این است که در گراف کامل 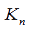 ، ، 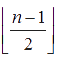 دور همیلتونی جدا از هم وجود دارد: دور همیلتونی جدا از هم وجود دارد: در مسأله n=9 است. بنابراین تعداد دورهای همیلتونی از رابطهی 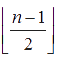 ، 4 تا میشود. در نتیجه بیشترین تعداد نامزدها 4تاست. ، 4 تا میشود. در نتیجه بیشترین تعداد نامزدها 4تاست. برای اثبات رابطهي 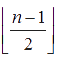 بهشکل ذيل عمل میکنیم: بهشکل ذيل عمل میکنیم: چون در گراف کامل 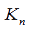 ، ، 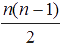 یال وجود دارد و هر دور همیلتونی n یال دارد حداکثر یال وجود دارد و هر دور همیلتونی n یال دارد حداکثر 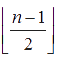 دور همیلتونی در دور همیلتونی در 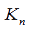 وجود دارد. وجود دارد.
حالتهای ذيل را در نظر میگیریم:
فرض کنید بهازای عدد طبیعی مانند: k ،n=2k+1 (چون حالت n=1 بیمعنی است). رأسهای 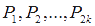 را بهترتیب در جهت ساعتگرد روی دایرهای به فاصلههای برابر میچینیم و رأس را بهترتیب در جهت ساعتگرد روی دایرهای به فاصلههای برابر میچینیم و رأس 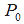 را در مرکز دایره قرار میدهیم. را در مرکز دایره قرار میدهیم.
اولین دور همیلتونی
است. میتوانیم این دور را با زاویههای 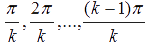 در جهت ساعتگرد بچرخانیم و k-1 دور دیگر بهدست بیاوریم که در مجموع تعداد دورها برابر میشود با: در جهت ساعتگرد بچرخانیم و k-1 دور دیگر بهدست بیاوریم که در مجموع تعداد دورها برابر میشود با:
فرض میکنیم که بهازای اعداد طبیعی مانند: k ،n=2k+2. رأسهای 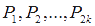 را بهترتیب در جهت ساعتگرد روی دایرهای به فاصلههای برابر میچینیم و رأس را بهترتیب در جهت ساعتگرد روی دایرهای به فاصلههای برابر میچینیم و رأس 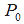 را در مرکز دایره قرار میدهیم. را در مرکز دایره قرار میدهیم.
میتوانیم رأس 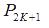 را جایی درون دایره قرار دهیم. در هر دور همیلتونی که در حالت 1 تعریف کردیم، را جایی درون دایره قرار دهیم. در هر دور همیلتونی که در حالت 1 تعریف کردیم، 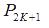 را سمت راست وسط این دور قرار میدهیم و به این ترتیب را سمت راست وسط این دور قرار میدهیم و به این ترتیب 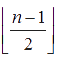 را بهدست میآوریم. را بهدست میآوریم. |