|
در مورد كدام‌يك از موضوعات مطرح شده مايل به كسب اطلاعات بيشتر هستيد؟
|
ارائه نظر |
|
| | راه‌هاي آسفالته (مسابقه‌ي شماره‌ي 50) |
| | راه‌هاي آسفالته (مسابقه‌ي شماره‌ي 50)مسابقه كامپيوتر | | | |  | | نظريه‌ي گراف ... سؤال همراه با جواب
| آن‌چه كه با عنوان «چكيده» در اول مسابقه‌ها و زنگ تفريح‌ها مشاهده مي‌كنيد صرفاً مخصوص معلمان، مربيان، كارشناسان محترم آموزشي و ساير علاقه‌مندان است.
 اهداف آموزشي
اهداف آموزشي در حوزه‌ي شناختي – دانش
- «دانش راه‌ها و وسايل برخورد با امور جزوي» > «دانش روش‌ها و روش‌شناسي»
- «دانش امور كلي و مسائل انتزاعي يك رشته» > «دانش اصل‌ها و تعميم‌ها»
اهداف آموزشي در حوزه‌ي شناختي - توانايي‌ها و مهارت‌هاي ذهني
- « فهميدن» < «تركيب» < «توليد يك نقشه يا مجموعه اقدام‌هاي پيشنهادي»
- « فهميدن» < «تركيب» < «استنتاج مجموعه‌اي از روابط انتزاعي»
نتايج مورد نظر
- آشنايي با نظريه‌ي گراف
- شناخت قضيه‌ي اولر
- چگونگي حل مسأله با استفاده از گراف‌ها
محتواي آموزشي
- نظريه گراف |
500 شهر در كشور فرضي «كانتري» وجود دارد. بعضي از شهرها با راه شوسه با يكديگر ارتباط دارند. امكان سفر از يك شهر به شهر ديگر از اين راه‌هاي شوسه وجود دارد.ثابت كنيد اگر دولت «كانتري» بخواهد بعضي از راه‌هاي شوسه را آسفالت كند مي‌تواند به‌گونه‌اي عمل كند كه هر شهر داراي تعداد فردي از راه‌هاي آسفالته باشد.
|
| راه حل اول
منظور از اصطلاح‌هاي شهر «فرد» و «زوج» شهرهايي است تعداد راه‌هاي آسفالته‌ي خروجي از آن شهرها به‌ترتيب «فرد» و «زوج» است. براي اين منظور از لمي با عنوان: «لم دوستي» (Handshake) استفاده مي‌كنيم؛ مطابق اين لم: «مهم نيست چه جاده‌هايي آسفالته هستند مهم آن است كه تعداد شهرهاي زوج، عددي «زوج» (ممكن است «صفر») باشد». براي بررسي صحت اين لم، فرض كنيد 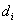 تعداد راه‌هاي آسفالته‌ي خروجي شهر .gif) باشد. مجموع راه‌هاي آسفالته‌ي خروجي كليه‌ي شهرها يعني: .gif) با دو برابر مجموع تعداد راه‌هاي خروجي كليه‌ي شهرها برابر است. فرض كنيد تعداد شهرهاي «زوج» عددي «فرد» باشد در اين‌صورت تعداد شهرهاي «زوج» عددي «فرد» مي‌شد (چون مجموع آن‌ها عددي «زوج» است). در اين مسأله 500 شهر وجود دارد و 500 نيز عددي «زوج» محسوب مي‌شود. اما طبق فرض جمع شهرهاي «زوج» بايد عددي «فرد» مي‌شد و اين يك تناقض است. با استفاده از «لم دوستي» (Handshake) مي‌توانيم الگوريتمي ايجاد كنيم كه سرانجام راه‌ها را به‌گونه‌اي آسفالت كند كه همه‌ي شهرها «فرد» باشند:
 |
راه حل دوم
كشور «كانتري» را يك گراف متصل (شبكه‌اي از رؤوس كه با يال‌هايي به هم متصل شده‌اند) در نظر مي‌گيريم كه در آن هر شهر يك «رأس» و هر جاده‌ي خاكي - كه دو شهر را به‌هم مرتبط مي‌كند – يك «يال» محسوب مي‌شود.
تعداد «رؤوس» عبارت است از:
براي هر .gif) هر مسيري از رأس .gif) را به رأس .gif) را درنظر مي‌گيريم (مي‌دانيم چنين مسيري وجود دارد زيرا گراف متصل است). سپس بر روي هر «يال» علامتي مي‌گذاريم تا مسير مذكور مشخص شود. هم‌چنين تمام راه‌ها (يال‌ها) را آسفالت مي‌كنيم تا اين‌كه تعداد علامت‌ها «زوج» باشد. براي اين‌كه نشان دهيم اين روش خواسته‌هاي ما را براورده مي‌كند كافي است ثابت كنيم براي يال‌هاي وابسته به هر رأس داراي تعداد «زوجي» از كليه‌ي علايم وجود دارد. بنابراين مجموع تعداد چنين يال‌هايي با تعداد «فردي» از علايم، عددي «فرد» خواهد بود. اما همه‌ي رويدادهاي رأس .gif) را در نظر بگيريد؛ يال‌هاي وابسته به رأس داراي تعداد «فردي» از علامت‌ها خواهند بود به‌خاطر اين‌كه مجموع تعداد چنين يال‌هايي با تعداد فردي از علامت‌ها عددي «فرد» خواهد بود. اما همه‌ي رويدادهاي رأس در هر يك از 500 مسير را در نظر بگيريد (توجه كنيد كه رأس پايان يكي از اين مسيرها است). بنابراين يكي از يال‌هاي وابسته به آن داراي علامت است. هر رويداد ديگر رأس بخش داخلي از يك مسير محسوب مي‌شود؛ بنابراين داراي دو علامت خواهد بود:
| - يكي در يال ورودي به رأس | | - ديگري در يال خروجي از آن. |
اين بدين‌معنا است كه كل تعداد علامت‌هاي وابسته به رأس عددي «فرد» است. بدين‌ترتيب مسأله ثابت مي‌شود. |
| |
| فرستنده : |
|
علیرضا شفائی |
 |
 |
1386/11/8 |
| | | | | مـتـن : |
من امشب توی این سکشن سایتتون یک گشتی زدم.باید اعتراف کنم که واقعا منبع کاملی است. واقعا بابت زحماتی که میکشید متشکرم
من تونستم 135 تا فایل PDF پیدا کنم روی سایتتون. از 0004 تا 0314
میخواستم بدونم اگر بیشتر مطالب علمی پیدا میشه آدرس بدید لطفا
و اینکه نگارش این PDF ها واقعا قشنگ بود.
مخصوصا در قسمت گراف. مثلا بقیه مطالب را در کتابهایی مثل استراتژی الفبا و .. دیده بودم ولی مطالب گراف را جایی نخونده بودم و به نظرم نحوه توضیحش بهتر از ترجمه های موجود بود.
یک نکته ی دیگه ای که برام سوال شده اینه که چرا دکمه داونلود PDF را خارج از کادر توی صفحه آموزش گذاشتید؟ اینطوری که هیچ کس بش دسترسی پیدا نمیکنه.
باتشکر
ع.ش | | | | | پاسـخ : | تاريخ ارسال: 1386/10/29
ايميل فرستنده: a.shafaei@gmail.com
عليرضا جان!
بخش آموزش المپياد دايما در حال تهيه و به‌روزرساني مطالب جديده. ضمن اين‌كه براي اين‌كه از مطالب PDf شده استفاده كني مي‌توني به بخش «پيوندها» مراجعه كرده وارد «مطالب آموزشي سايت» بشي. در اين صورت فايل‌هاي مذكور با يك Save as در اختيارتون قرا مي‌گيره.
باز هم از حضور فعالت تشكر مي‌كنيم.
دوست داري با بچه‌هاي ما همكاري داشته باشي؟
منتظر جوابت هستيم. | | | |
|
|
| | فرستنده : |
|
علیرضا شفائی |
|
|
1386/11/8 |
| | | | | مـتـن : |
خیلی مسئله ی قشنگی بود. واقعا از اینکه زحمت میکشید و مسئله در این سایت میزارید متشکرم.!
من این مسئله را اومدم اینطوری با یک گراف متناظر کردم.
هر شهر معادل روس و مسیرهای شوسه بین اونها هم یالهاست.گراف مون همبنده . میخواییم یک زیرگراف انتخاب کنیم که توی اون هر راس درجه اش فرد باشه.
روش کلی اثبات استقرائه و از رفیق جدیدمون یعنی Contraction یا منقبض کردن کمک میگیرم.
لم: هر گراف همبند باید حداقل n-1 یال داشته باشه.
اثبات: میخوام از فرمولی که در سوال هفته پیش به کار رفته برای اثبات استفاده کنم. اثبات کردم
n-e+f=k+1
گفتیم گرافمون همبنده پس k=1
گفتیم با حداقل یال پس دور نداره پس تعداد ناحیه ها =1 چون اگر دور داشته باشه میشه یک یال از دور حذف کرد و گراف همچنان همبند باقی بمونه(دلیلش تابلوئه برای همین وقتتون را نمیگیرم) و این هم تناقضه با فرض اولیه. پس داریم f=1
با جایگزاری در معادله بالا نتیجه میشه
e=n-1
پس لم مون اثبات شد D:
تعریف منقبض کردن یال را هم اگر یادتون رفته بدونید اینه که میاییم یک یال را انقدر منقبض میکنیم تا دو راس متصل به اون روی هم بیوفتن!
اثبات مسئله اصلی:
استقرا روی تعداد روس. برای n=2 یک یال داریم(حداقل طبق لم یک یال داریم) که ایندو رو به هم متصل کرده با انتخاب این یال صورت مسئله صحیح باقی میمونه و درجه هر دوراس فرد میمونه.
فرض میکنیم برای n هم درست باشه. میریم سر n+2
توی این گراف راسی داریم که درجه اش حداقل 2 باشه.
دلیل!. اگر درجه همه ی روس کمتر از دو باشه نتیجه میشه که تعداد یالها هم کمتر از n-1 است. و این با فرض مسئله و لم اثبات شده در تناقضه.
میاییم اون یال که درجه اش حداقل دو است را انتخاب میکنیم. اسمش را میزاریم A
گراف 'g را اینطوری میسازیم. یال مرتبط کننده با دوهمسایه B و C را منقبض میکنیم. اینطوری دو راس از گرافمون کم میشه و یک گراف N راسی داریم که با شرایط صدق میکنه. طبق فرض این گراف یک زیرگراف داره که با صورت مسئله در اون صدق میکنه. حالا میاییم توی گراف اولیه مون یعنی g یالهایی که در زیرگراف 'g بوده را در گراف g انتخاب میکنیم.(همون یالهای جواب n راسی) اگر در زیرگراف 'g یالی انتخاب شده بود که قبلا در یکی از رووس Bیا C بود باید در g همون یال را انتخاب کنیم (اگر متوجه شدن سخته میتونید اینطوری تصور کنید که زیرگراف 'g را منبسط میکنیم روی همون راس تا بشه مثله قبل). حالا درجه سه تا از روس A و B و C عوض میشه ولی بقیه روس همچنان فرد میمونن چون اصلا با یالهای اونا کاری نداشتیم. اگر درجه را با Dv نشون بدیم . میدانیم که Da+Db+Dc عدد فردی است چون وقتی منقبض شده بودن تا گراف N راسی را بسازیم در زیرگرافمون درجه جدید A فرد بوده و در اصل درجه A مجموعه درجات روس b و c بوده.حالا که منقبض کردیم Da+Db+Dc باید فرد باشه!.
میدونیم که یال AB و AC وجود دارد.(اول کار گفتم که راسی را انتخاب میکنیم که درجش حداقل دو باشه . بعد دوتا از همسایه هاش را به نام B و C ور میداریم. این دوتا یالی که گفتم یال متصل کننده این راس به همسایه هاشه)
وقتی یال AB و AC وجود داشته باشه. هر کدوم Da Db Dc که فرد نباشه میشه از یالهای AB و AC برای فرد کردن همه ی درجات استفاده کرد. 3 حالت کلا میشه
یکی از حالتهای ممکن اینه.
Da زوج Db فرد Dc زوج (باید جمعشون فرد باشه)(یا به طور کلی Da زوج یکی شون فرد و یکی دیگشون زوج)
در این حالت میشه یال AC را اضافه کرد در زیرگرافمون تا درجه همشون بشه فرد.
Da فرد Db زوج Dc زوج
در این حالت کافیه هر دو یال AB و AC اضافه بشه
اگر هرسه درجشون فرد باشه که اصلا نیاز به AB و AC نیست
پس برای N+2 هم اثبات شد. ازاونجایی که پایه زوجه برای تمام اعداد زوج اثبات میشه
خیلی طولانی شد ببخشید
با تشکر
ع.ش | | | | | پاسـخ : | ايميل فرستنده: a.shafaei@gmail.com
تاريخ ارسال: 1386/10/27
عليرضا جان!
مثل هميشه جوابت كاملا درسته. تو يه جورايي به ساير بچه‌ها هم داري كمك مي‌كني بنابراين در نهايت به ما كمك مي‌كني.
واقعا از اين كه اين سايت رو مال خودت مي‌دوني و تو مسابقه شركت مي‌كني تشكر مي‌كنيم.
موفق باشي! | | | |
|
|
| | فرستنده : |
|
Kherad |
|
|
1386/11/8 |
| | | | | مـتـن : |
بالاخره امتحانای ترم تموم شد !
چند تا تعریف :
گراف ساده : مجومه ی V = {x1,x2,x3....,xn و E = {{xi1,xj1},{xi2,xj2},...,{xim,xjm
برای نمایش گراف ساده به ازای هر عضو V یک نقطه (راس) و به ازای هر عضو v یک خط (یال) بین دو راس xi و xj آن عضو می گذاریم
گشت : مجومه ی e= {xi1,xi2,xi3,...{ که بین هر دو xi متوالی در این مجموعه یال هست .
دور : گشتی که اول و آخر آن یک راس باشد .
مسیر : گشتی که دور نداشته باشد .
درجه ی هر راس : تعداد یال هایی که بر هر راس متصل است .
گراف همبند : گرافی که بین هر دو راس آن مسیر وجود دارد .
درخت : گراف همبند بدون دور .
زیر گراف : گرافی با مجوعه راس e و مجموعه یال v به طوری که e , v زیر مجموعه ی E و V باشند .
(این همه توضیح دادم آخرش می بینی سوال رو اشتباه حل کردم !)
-------------------------
خوب ما به ازای هر شهر یک راس و به ازای هر مسیر بین دو شهر یال بین راس آن دو شهر می ذاریم .
از هر شهر می شه به شهر دیگه رفت . یعنی گراف همبند هست . در واقع بین هر دو راس گذر هست که با استقرا ثابت می شه مسیر هم وجود داره .
دوباره (فکر کنم با استقرا ) ثابت می شه که از هر گراف همبند می شه یک زیر گراف ساخت به طوری که درخت باشه .
برای که بگیم روی این درخت می شه آسفالت کشی مورد نظر رو انجام داد استقرا می زنیم روی تعداد راس های زوج
برای تعداد راس های 2 که چون فقط یک یال هست درسته .
حالا فرض می کنیم واسه همه تعداد راس های زوج کوچکتر از n وجود داشته باشه حالا می خوایم بگیم واسه n که زوج هست وجود داره .
در درخت n راسیمون یک برگ (راسی با درجه ی 1 ) و راس مجاورش (راسی که برگ بهش راه داره (راستی معلومه که برگ فقط به یک راس یال داره چون در غیر این صورت برگ نیست ))
رو انتخاب می کنیم . اگر به اون راس فقط همین برگ وصل بود که بین این 2 تا آسفالت می کشیم و بی خال این دو تا راس می شیم طبق استقرا واسه n-2 داریم پس حله
اما اگر غیر از این برگ به برگ های دیگه هم یال داشت اگه تعداد برگ هایی که به این وصل هستند فرد باشه که دوباره مثل قبل حله اما اگه زوج باشه با خود اون راسه می شه فرد اما چون تعداد کل راس های ما زوج هست پس ل یه راس دیگه هست . که این راس به اون یال داره . حالا ما مجوعه ی همه ی اینا رو می گیرم (یعنی اون برگ ها (که تعدادشون زوج بود) اون راسی که همه ی برگ ها به اون وصل بودند و اون راسی که به این راس وصل بود ) که تعدادشون زوج هست . بین همه ی اون برگ ها و راس مجاور مشارکشون راه آسفلته می کشیم و بین اون راس مجاور مشترک و راسی که بهش وصله (غیر از برگ ها ) راه آسفالته می کشیم . که تا الان درجه ی این راس ها فرد شده .
حالا چون تعداشون زوجه بی خیالشون می شیم . برای بقیه ی راس ها طبق استقرا همچین آسفالت کشی داریم .
پس حل شد . چون 500 یه عدد زوجه .
البته فکر کنم اینو با جورسازی هم بشه حل کرد . به طوری که ما واسه درختمون (که چون درخت هست دور فرد نداره و دو بخشی هست و شرط لازم واسه مچینگ کامل هم توش برقراره(همسایه های هر راس مجموعه راس از بخش پایین بیشتر مساویه تعداد همون مجموعه راس هست )) ما یک مچینگ کامل داریم .
چقد ضد حاله همه اینا اشتباه باشه !
جواب تاريخ: 1386/11/4
سلام ... من شک کردم که نوشته ها برای شما فرستاده شده یا نه برای همین یک بار دیگه می فرستم .
بالاخره امتحانای ترم تموم شد !
چند تا تعریف :
گراف ساده : مجومه ی V = {x1,x2,x3....,xn و E = {{xi1,xj1},{xi2,xj2},...,{xim,xjm
برای نمایش گراف ساده به ازای هر عضو V یک نقطه (راس) و به ازای هر عضو v یک خط (یال) بین دو راس xi و xj آن عضو می گذاریم
گشت : مجومه ی e= {xi1,xi2,xi3,...{ که بین هر دو xi متوالی در این مجموعه یال هست .
دور : گشتی که اول و آخر آن یک راس باشد .
مسیر : گشتی که دور نداشته باشد .
درجه ی هر راس : تعداد یال هایی که بر هر راس متصل است .
گراف همبند : گرافی که بین هر دو راس آن مسیر وجود دارد .
درخت : گراف همبند بدون دور .
زیر گراف : گرافی با مجوعه راس e و مجموعه یال v به طوری که e , v زیر مجموعه ی E و V باشند .
(این همه توضیح دادم آخرش می بینی سوال رو اشتباه حل کردم !)
-------------------------
خوب ما به ازای هر شهر یک راس و به ازای هر مسیر بین دو شهر یال بین راس آن دو شهر می ذاریم .
از هر شهر می شه به شهر دیگه رفت . یعنی گراف همبند هست . در واقع بین هر دو راس گذر هست که با استقرا ثابت می شه مسیر هم وجود داره .
دوباره (فکر کنم با استقرا ) ثابت می شه که از هر گراف همبند می شه یک زیر گراف ساخت به طوری که درخت باشه .
برای که بگیم روی این درخت می شه آسفالت کشی مورد نظر رو انجام داد استقرا می زنیم روی تعداد راس های زوج
برای تعداد راس های 2 که چون فقط یک یال هست درسته .
حالا فرض می کنیم واسه همه تعداد راس های زوج کوچکتر از n وجود داشته باشه حالا می خوایم بگیم واسه n که زوج هست وجود داره .
در درخت n راسیمون یک برگ (راسی با درجه ی 1 ) و راس مجاورش (راسی که برگ بهش راه داره (راستی معلومه که برگ فقط به یک راس یال داره چون در غیر این صورت برگ نیست ))
رو انتخاب می کنیم . اگر به اون راس فقط همین برگ وصل بود که بین این 2 تا آسفالت می کشیم و بی خال این دو تا راس می شیم طبق استقرا واسه n-2 داریم پس حله
اما اگر غیر از این برگ به برگ های دیگه هم یال داشت اگه تعداد برگ هایی که به این وصل هستند فرد باشه که دوباره مثل قبل حله اما اگه زوج باشه با خود اون راسه می شه فرد اما چون تعداد کل راس های ما زوج هست پس ل یه راس دیگه هست . که این راس به اون یال داره . حالا ما مجوعه ی همه ی اینا رو می گیرم (یعنی اون برگ ها (که تعدادشون زوج بود) اون راسی که همه ی برگ ها به اون وصل بودند و اون راسی که به این راس وصل بود ) که تعدادشون زوج هست . بین همه ی اون برگ ها و راس مجاور مشارکشون راه آسفلته می کشیم و بین اون راس مجاور مشترک و راسی که بهش وصله (غیر از برگ ها ) راه آسفالته می کشیم . که تا الان درجه ی این راس ها فرد شده .
حالا چون تعداشون زوجه بی خیالشون می شیم . برای بقیه ی راس ها طبق استقرا همچین آسفالت کشی داریم .
پس حل شد . چون 500 یه عدد زوجه . | | | | | پاسـخ : | ايمل فرستنده: a.i.kheradmand@gmail.com
تاريخ ارسال: 1386/10/29
خردمند جان!
جوابت كاملا صحيح و دقيقه. از جواب كاملت تشكر مي‌كنيم.
درود بر شما! آفرين!
انشاءالله در همه‌ي صحنه‌هاي زندگي موفق باشي! | | | |
|
|
| | فرستنده : |
|
ناشناس |
|
|
1386/11/8 |
| | | | | مـتـن : |
با سلام،
اگر چیدمان شهر های کشور را این گونه فرض کنیم:
لینک تصویر:http://iranx.110mb.com/All_Steps.JPG
همان طور که مسئله بیان کرده است کشور در حال حاضر بگونه ای است که می توان از شهری به شهر دیگری فقط از طریق راه شوسه سفر کرد.
پس آرایش کشور می تواند این گونه باشد:(فقط راه های شوسه)
لینک تصویر : http://iranx.110mb.com/Step1.JPG
و این گونه:
http://iranx.110mb.com/Ste2.5.JPG
حال اگر بخواهیم برخی از راه های شوسه آسفالت کنیم به طوری که هر شهر دارای تعداد فردی از راه های شوسه باشد باید،به صورت تصویر زیر عمل کنیم:
لینک تصویر: http://iranx.110mb.com/Step2.JPG
حال می بینیم که هر شهر دارای تعداد فردی از راه های آسفالته است.
امیدوارم درست باشد....
ممنون | | | | | پاسـخ : | ايميل فرستنده: xsx_vbs@yahoo.com
تاريخ ارسال: 1386/10/27
دوست خوبم!
اين‌كه مسأله رو به‌صورت يك شكل دراوردي كار بسيار زيبايي انجام دادي. در واقع مسائل انتزاعي رو به‌صورت شكلي قابل‌فهم ارائه كردي. اين‌كار شما خيلي تحسين‌برانگيزه.
اما دوست خوبم بايد به استدلال تحسين‌برانگيز شما اين رو هم اضافه كرد كه ممكنه شهرهاي غيرمجاور با راه‌هايي به‌هم مرتبط بشن.
درود بر شما! آفرين!
انشاءالله بيش از پيش موفق باشي! | | | |
|
|
|
|
|
| |  | كاربران غيرعضو آنلاين: 2 | | | كاربران عضو آنلاين: 0 | | | کل كاربران آنلاين: 2 |
|
|
|
|